内部自发热及对流的一维复合壁面

系统

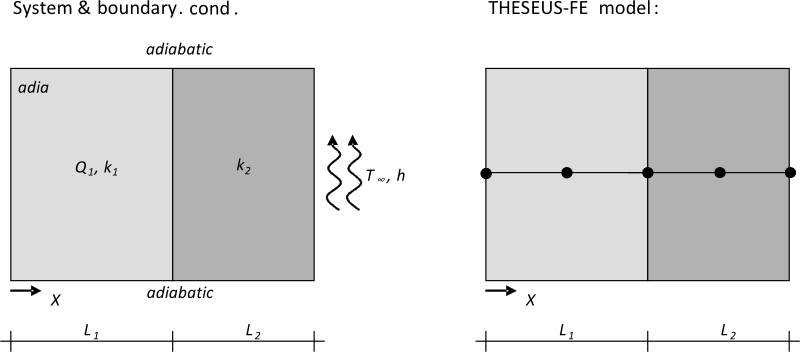
系统及边界条件

参数 数值 单位 描述
Q 1 1.5E6 W / m 3 发热量
k 1 75 W / m*K 左侧导热系数
L 1 0.05 m 左侧厚度
k 2 150 W / m*K 右侧导热系数
L 2 0.02 m 右侧厚度
h 1000 W / m 2 *K 对流换热系数
T ∞ 30 °C 环境温度

问题描述

建立了一个在第一层发热的双层复合壁面模型。复合壁面一面是绝热的，另一面具有对流边界条件。温度分布的精确分析解见参考书目[1]。

THESEUS‑FE模型

1个有2层和每层6个离散点的四边形壳网格（PSHELL）。

说明

该问题也被建模为2层和每层3个离散点，结果与更高数量的离散点一样准确。

结果

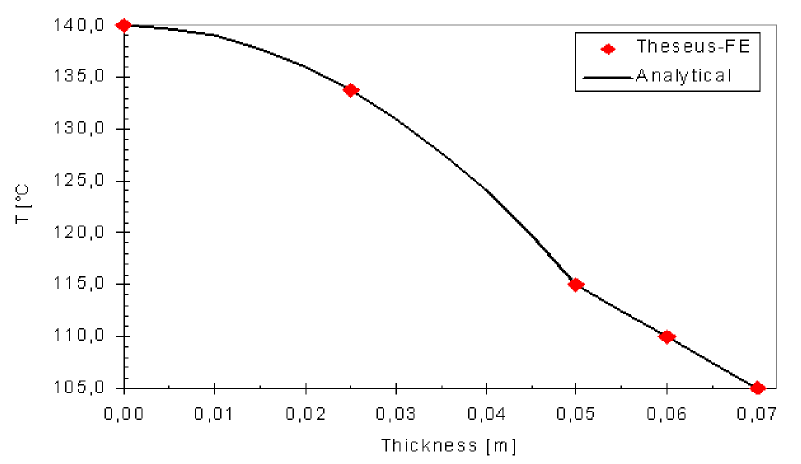
矩形平板的二维传导

系统

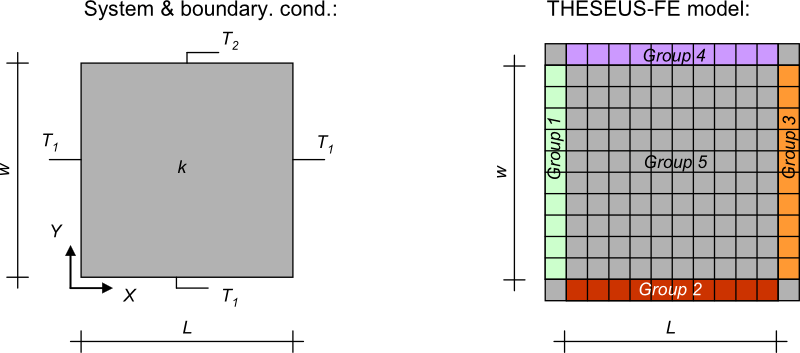
系统和边界条件

参数 数值 单位 描述
k 81 W / m*K 导热系数
L 0.833 m 长度
w 0.83 m 宽度
T 1 100 °C 温度边界条件
T 2 20 °C 温度边界条件

问题描述

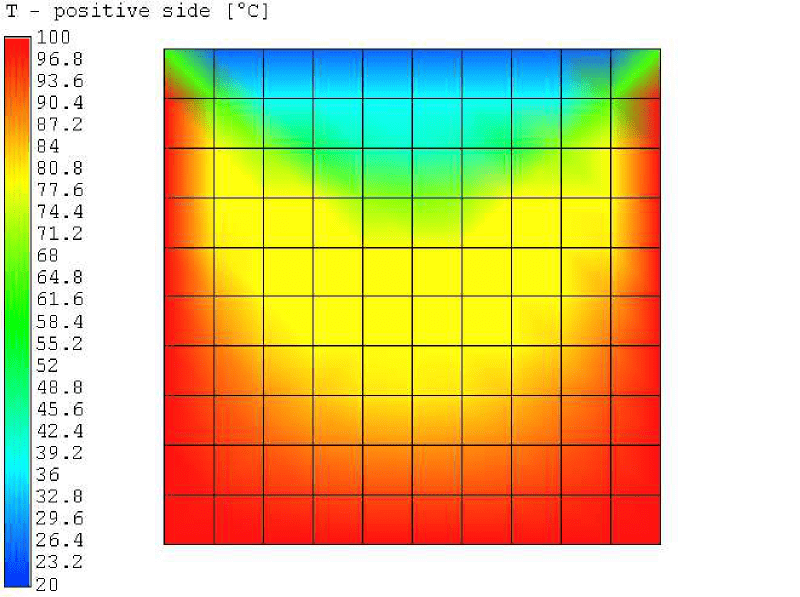
对二维矩形进行了建模，并在所有4个边上进行了温度边界条件模拟。参考书目[2]给出了精确的分析解。

THESEUS‑FE模型

使用12*12 PSHELL3网格对矩形进行建模；每个网格在厚度方向上有1层和2个离散点来表示上面和底面。有限元模型的长度和宽度比实际长度要长，以设置1到4组表面的温度边界条件。第5组表示温度作为位置函数计算的域。

结果

在x=0.0833和x=0.5处的结果
温度云图

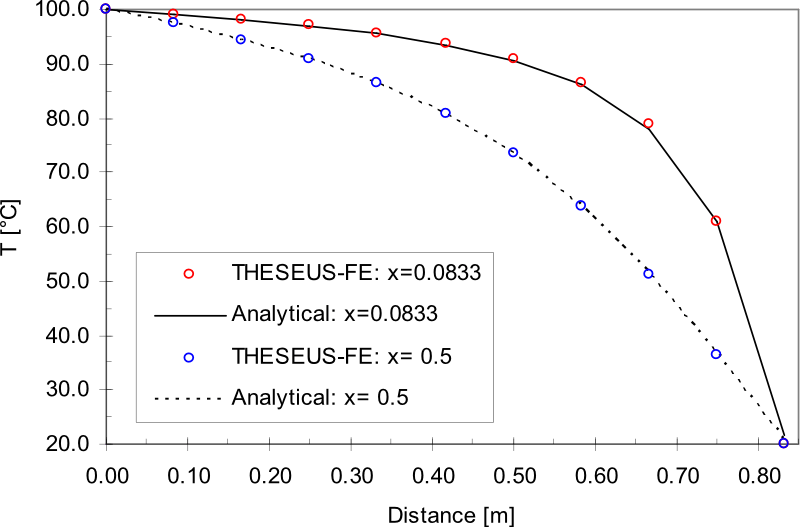
圆盘上的二维传导

系统

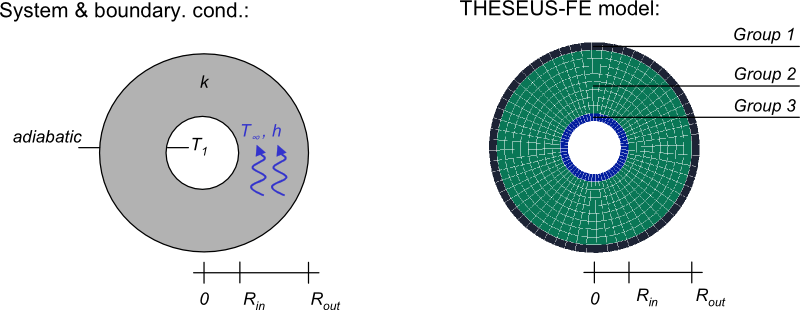
系统和边界条件

参数 数值 单位 描述
k 81 W / m*K 导热系数
R in 0.065 m 内径
R out 0.185 m 外径
T 1 50 °C 内边缘的温度
h 100 W / m 2 *K 对流换热系数
T ∞ 20 °C 环境温度

问题描述

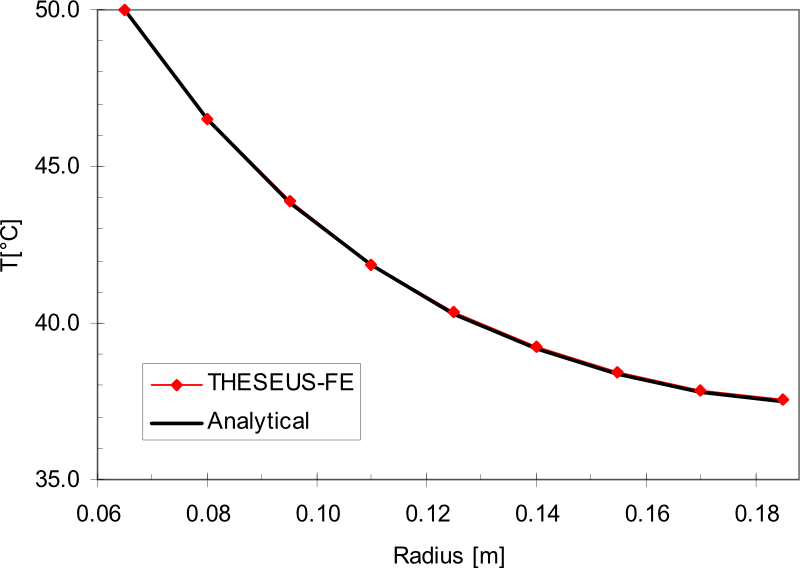
对一个半径为0.065m的二维圆盘设置内边缘温度边界条件和外边缘绝热条件的模拟。对流边界条件适用于圆盘的其余部分。参考书目[2]给出了精确的分析解。

THESEUS‑FE模型

使用3个不同的组对圆盘进行建模，每个元素是一个在厚度方向上有1层和2个离散点来表示顶面和底面的PSHELL3网格。有限元模型的内径比实际短，外径比实际长，用于设置边界条件（第1组和第3组）。第2组表示温度作为位置函数计算的域。

结果

温度vs半径
温度云图

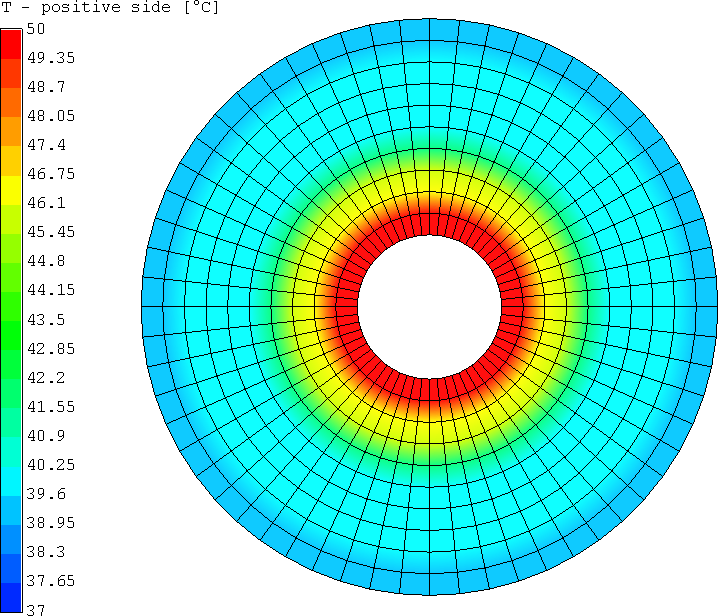
球体加热

系统

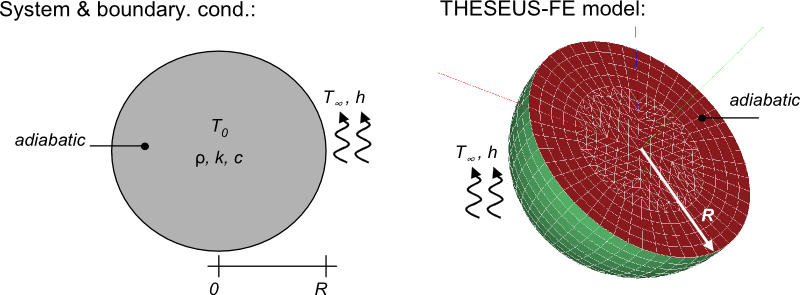
系统和边界条件

参数 数值 单位 描述
k 50 W / m*K 导热系数
ρ 8000 kg / m 3 密度
c 500 J / kg*K 比热容
R 0.1 m 半径
h 100 W / m 2 *K 传热系数
T ∞ 100 °C 环境温度
T 0 20 °C 初始温度

问题描述

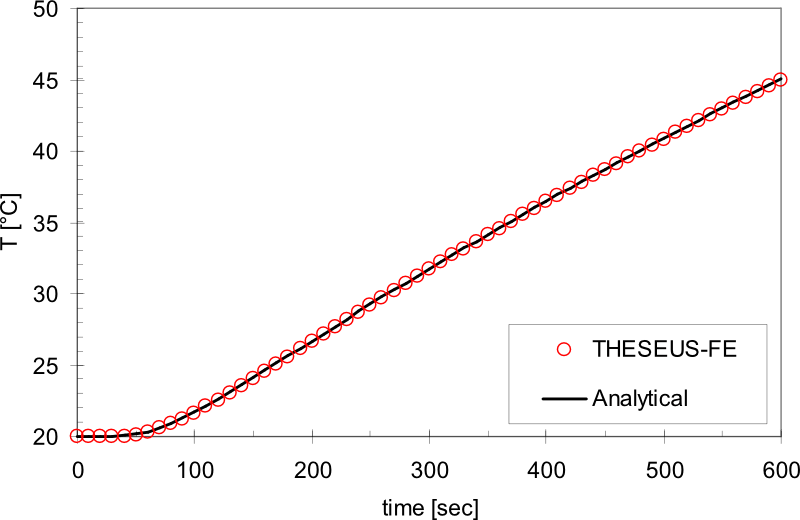
随着时间的推移，初始温度为T0的球体被对流环境温度加热的模拟。参考书目[3] 给出了精确的分析解。

THESEUS‑FE模型

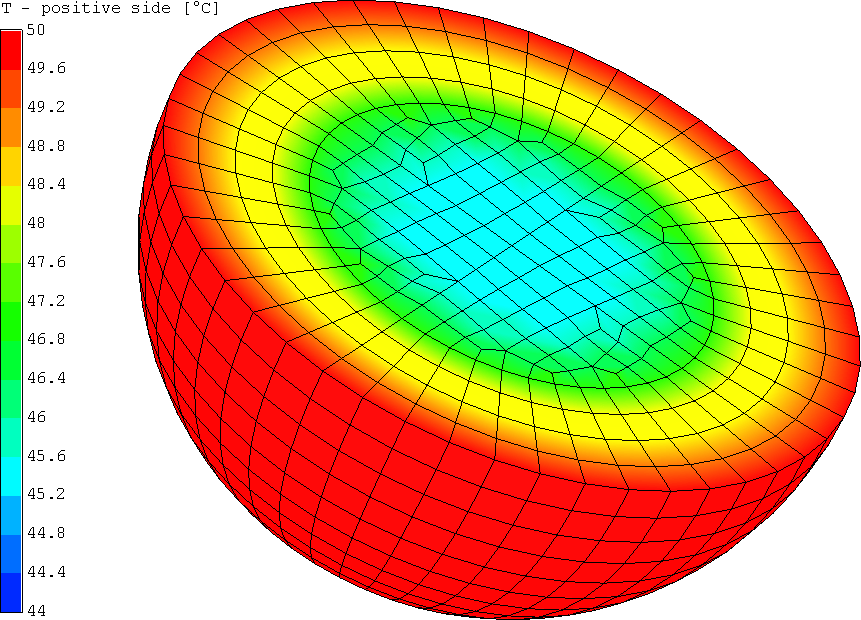
用3组模型模拟问题；组1是中心面（PSHELL3）应用绝热边界条件，组2是外表面（PSHELL3）应用对流，组3是由六边形网格组成的内部实体。

结果

随时间变化的中心节点结果
T=600s时的温度云图

圆柱体加热

系统

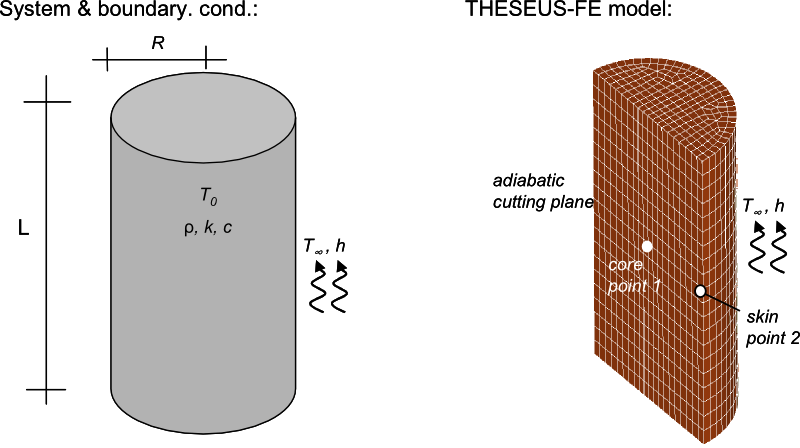
系统和边界条件

参数 数值 单位 描述
k 58 W / m*K 导热系数
ρ 8000 kg / m 3 密度
c 545 J / kg*K 比热容
L 0.3 m 长度
R 0.1 m 半径
h 20 W / m 2 *K 对流换热系数
T ∞ 800 °C 环境温度
T 0 25 °C 初始温度

问题描述

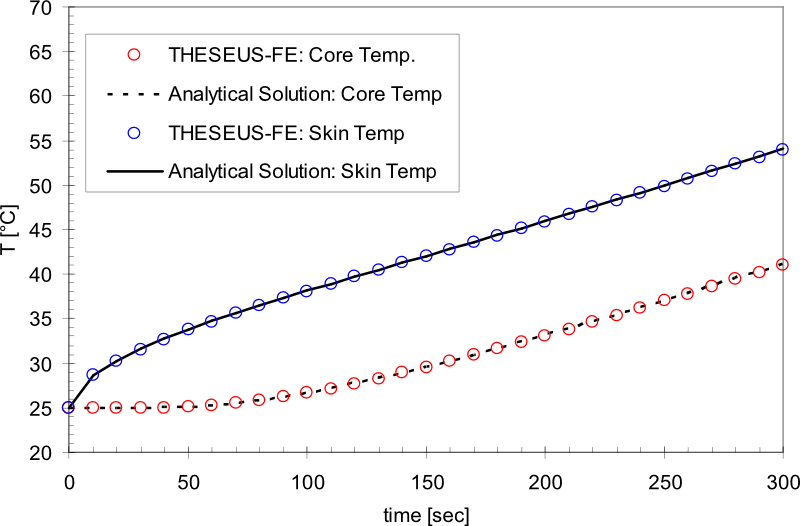
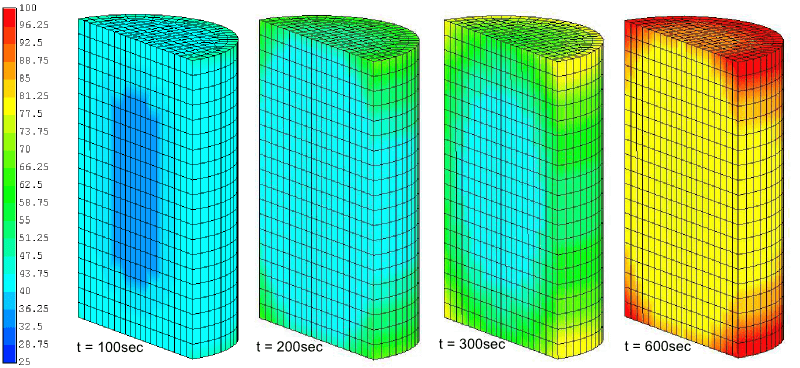
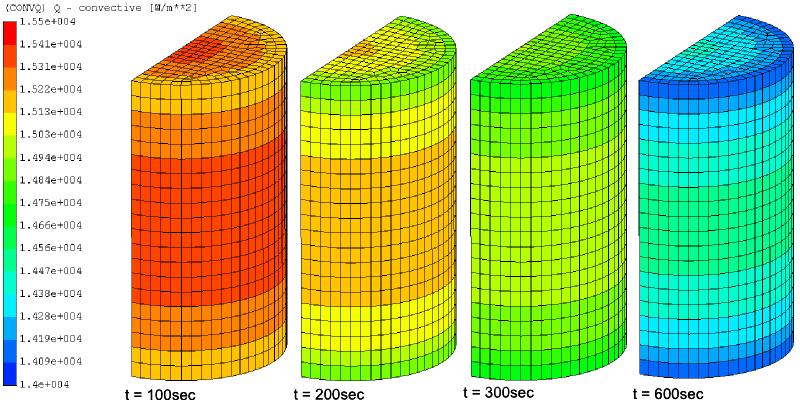
一个初始温度为T0的圆柱体温度随着时间的推移被环境温度加热的模拟。参考书目[3] 给出了精确的分析解。

THESEUS‑FE模型

用3组模型模拟问题；组1是中心面（PSHELL3）应用绝热边界条件的中心面，组2是外表面（PSHELL3）应用对流的，组3是由六边形网格组成的内部实体。

结果

核心和表面的结果（t=0…300s）
核心和表面的结果（t=0…22500s）
温度云图
对流热流密度云图

无限体内部的热脉冲

系统

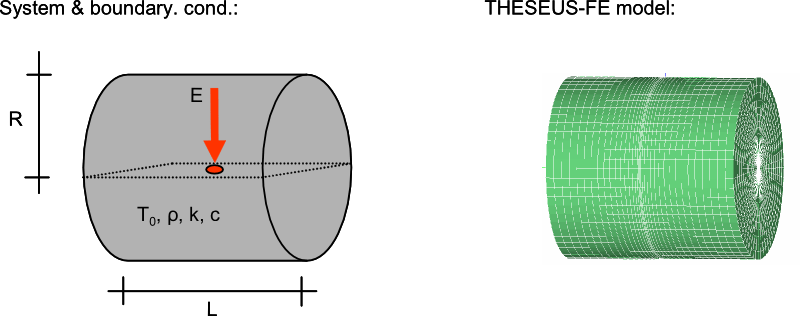
系统和边界条件

参数 数值 单位 描述
k 50 W / m*K 导热系数
ρ 10000 kg / m 3 密度
c 500 J / kg*K 比热容
L 0.6 m 长度
R 0.3 m 半径
E 22643.38 J 初始输入能量
T 0 0 °C 初始温度

问题描述

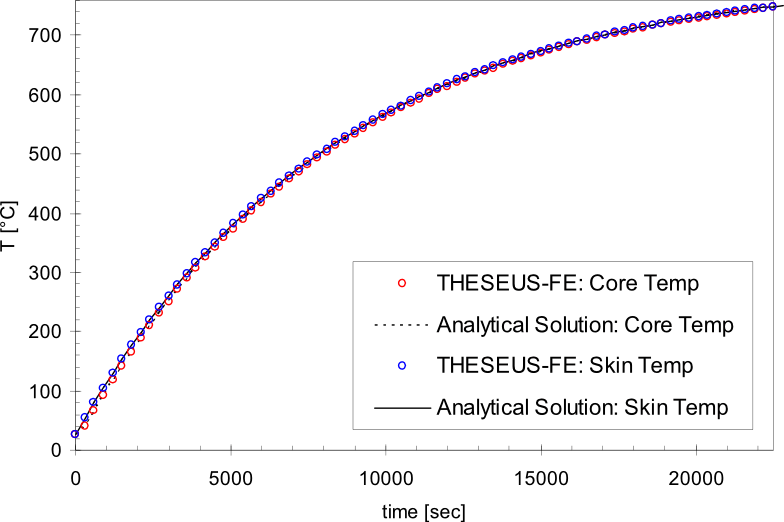
建立了一个Dirac内热脉冲作用下的圆柱模型。参考书目[3]给出了精确的分析解。

THESEUS‑FE模型

该问题由两组进行建模。热脉冲施加在第1组的内部面积2.26E-5 m2的PSHELL3网格上，持续时间为1秒。第2组是一个实体单元网格，用作圆柱体的主体。该圆柱体足够大，用来表示点载荷作用下的无限固体。

结果

t = 20 s 和 t = 100 s的结果
R=0时随时间变化的结果
温度云图

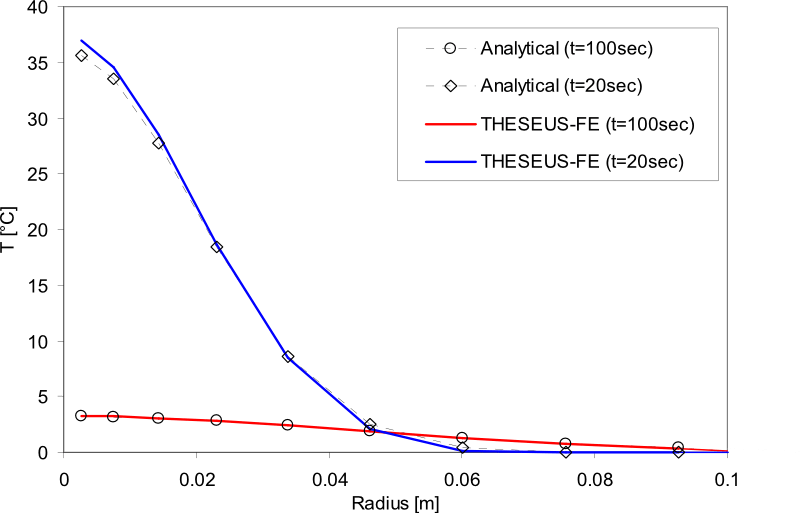
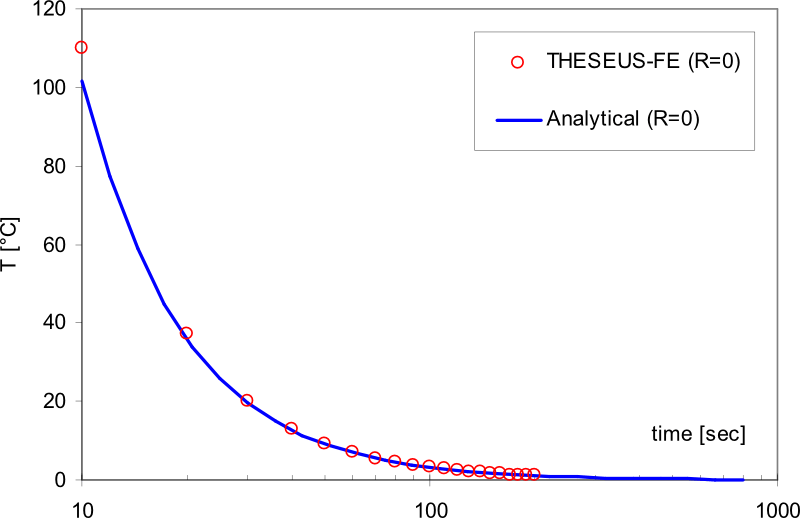
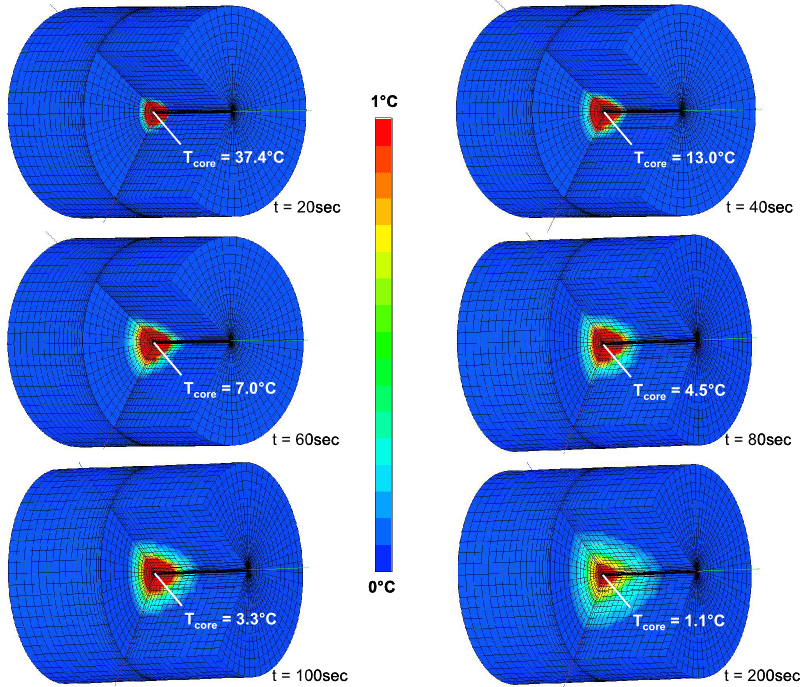
参考书目

[1]  INCROPERA, F.P., DEWITT, D.P., Fundamentals of heat and mass transfer, John Wiley & Son, New York, 1996.
[2]  MYERS, G.E., Analytical methods in conduction heat transfer, Genium Publishing Corporation, New York, 1987.
[3]  BAEHR, H.D, STEPHAN, K., Heat and mass transfer, Springer, Berlin, 1998.