热桥
系统
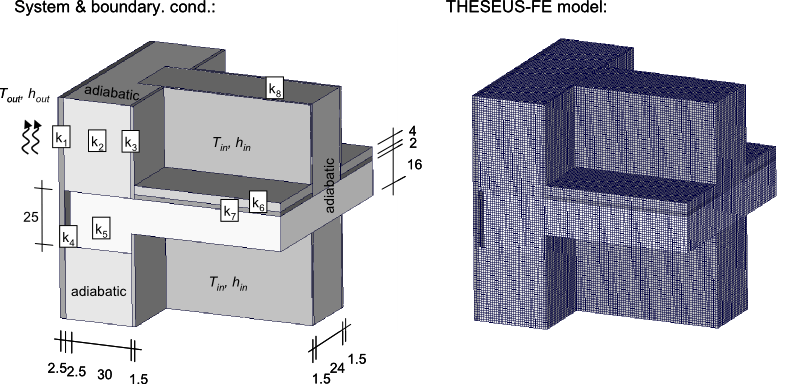
系统和边界条件
| 参数 | 数值 | 单位 | 描述 |
|---|---|---|---|
| k 1 | 0.87 | W / m*K | 导热系数 |
| k 2 | 0.21 | W / m*K | 导热系数 |
| k 3 | 0.35 | W / m*K | 导热系数 |
| k 4 | 0.093 | W / m*K | 导热系数 |
| k 5 | 2.1 | W / m*K | 导热系数 |
| k 6 | 1.4 | W / m*K | 导热系数 |
| k 7 | 0.04 | W / m*K | 导热系数 |
| k 8 | 0.7 | W / m*K | 导热系数 |
| T out | 5 | °C | 外部空气温度 |
| h out | 25 | W / m 2 *K | 对流换热系数 |
| T in | 22 | °C | 内部空气温度 |
| h in | 5 | W / m 2 *K | 对流换热系数 |
问题描述
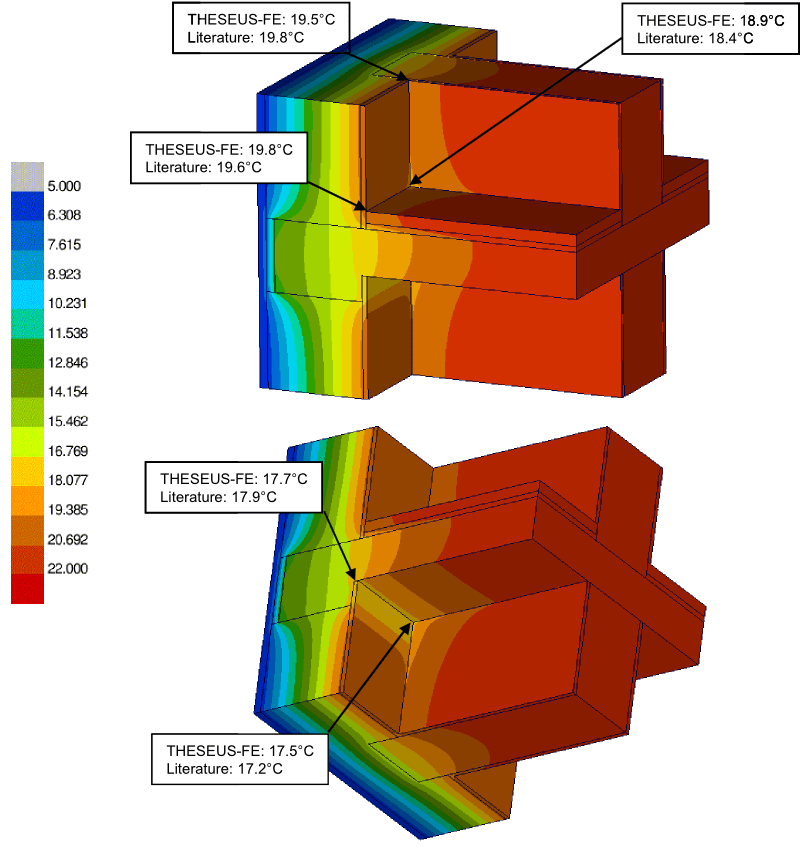
通过复合墙体进行热传导的三维热桥示例。墙体的内外表面被设定为对流边界条件。对比THESEUS‑FE与在多个拐角和沿边缘位置的实验结果[1]。
THESEUS‑FE模型
该问题由八组实体网格(代表复合壁面的不同部分)和两组PSHELL3网格建模。壳单元网格放置在内外表面上,用于指定对流边界条件。采用长度约为1cm的四边形均匀网格,共有390276个网格。
结果
各向异性导热系数
系统
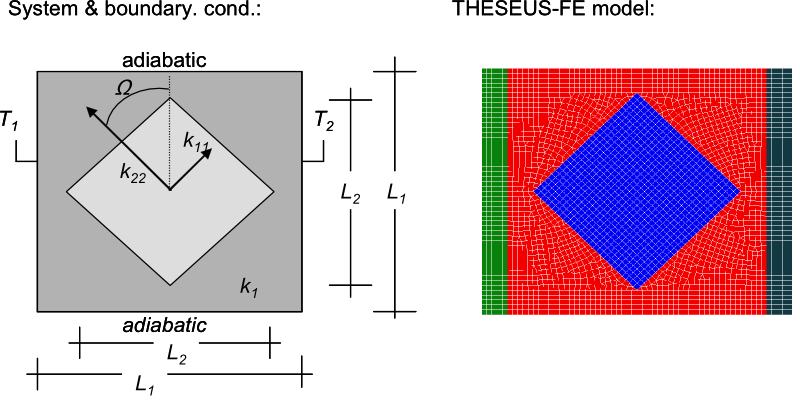
系统和边界条件
| 参数 | 数值 | 单位 | 描述 |
|---|---|---|---|
| k 1 | 0.56 | W / m*K | 导热系数 |
| k 11 | 0.056 | W / m*K | 导热系数 |
| k 22 | 0.0056 | W / m*K | 导热系数 |
| T 1 | 100 | °C | 温度边界条件 |
| T 2 | 0 | °C | 温度边界条件 |
| L 1 | 1 | m | 长度 |
| L 2 | 0.8 | m | 长度 |
| Ω | 45 | Degrees | 旋转角度 |
问题描述
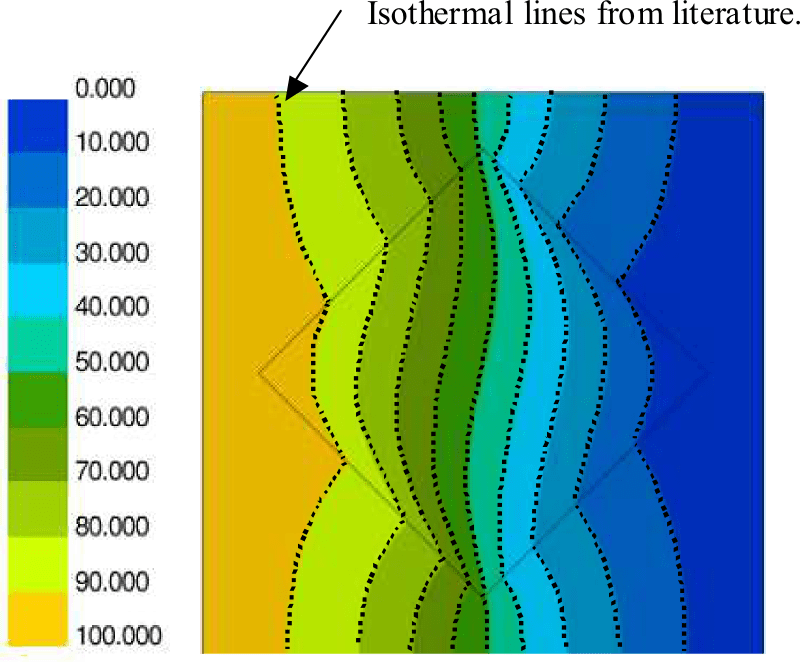
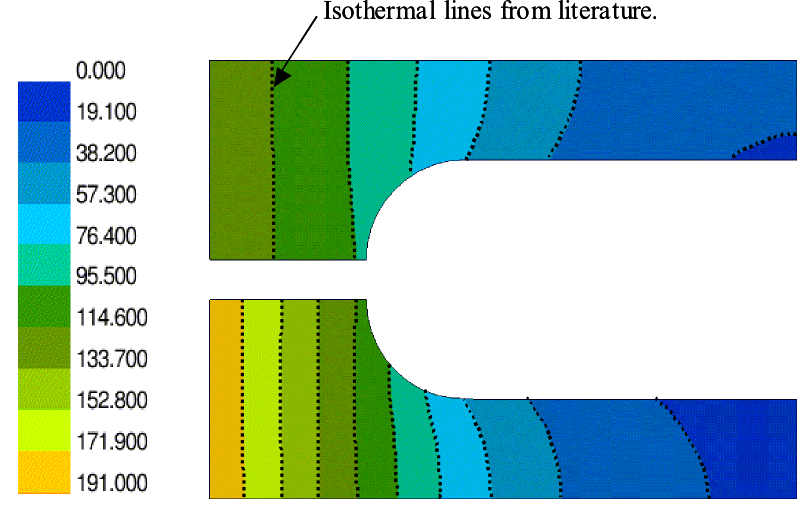
利用一个带有倾斜方形嵌件的平面正方形来演示各向异性导热系数的影响。参考图3,外正方形是导热系数为k1的各向同性材料。在水平边缘绝缘的情况下,对正方形的垂直边缘施加恒温边界条件。内部材料为正交异性,k11=k1/10,k22=k1/100。材料轴相对于全局坐标轴的方向为45度。图4显示了温度场。结果由于各向异性而产生的失真清晰可见。虚线是文献中用于验证的等温线[2]。
THESEUS‑FE模型
该问题由四组PHSHELL3网格建模。温度边界条件设置在左右垂直组上。外部网格设定为各向同性材料,而内部网格以局部坐标的张量形式设置为各向异性材料。
结果
随温度变化的导热系数
系统
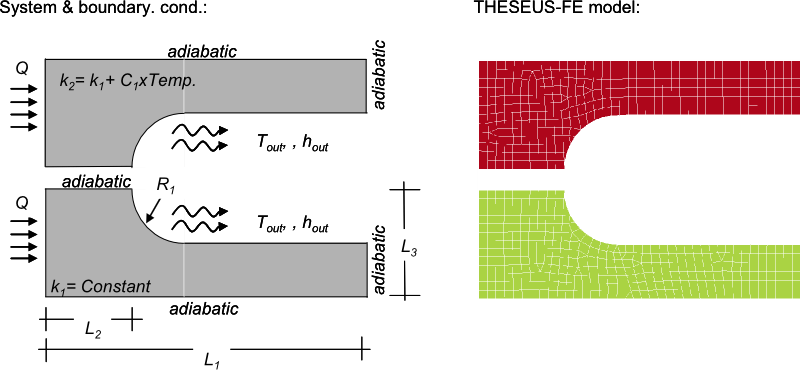
系统和边界条件
| 参数 | 数值 | 单位 | 描述 |
|---|---|---|---|
| k 1 | 1 | W / m*K | 导热系数 |
| C 1 | 0.01 | 常数 | |
| T out | 0 | °C | 温度边界条件 |
| h out | 0.875 | W / m 2 *K | 对流换热系数 |
| L 1 | 3 | m | 长度 |
| L 2 | 0.8 | m | 长度 |
| L 3 | 1 | m | 长度 |
| R 1 | 0.5 | m | 半径 |
| Q | 100 | W / m 2 | 热流密度 |
问题描述
这个例子说明了当模型中包含变导热系数时结果的差异。图5包含一个简单平面几何图形的示意图和网格。上下半部分被不同的各向同性材料占据;下半部分材料具有恒定的导热系数k1,同时材料具有随温度变化的导热系数k=k1+c1*t。沿区域的左边缘施加恒定的热流。右侧边界是绝热的。所有其他表面均通过恒定的对流换热系数和流体温度进行对流冷却[2]。
THESEUS‑FE模型
用两组任意厚度的实体网格和四组PSHELL3网格对该问题进行了建模。给壳单元网格设定热流密度和对流边界条件。使用瞬态二阶求解器,初始时间步长为0.1秒,运行时间为25秒。第二组固体网格的导热系数是可变的。
结果
相变
系统

系统和边界条件
问题描述
| 参数 | 数值 | 单位 | 描述 |
|---|---|---|---|
| k 1 | 1.08 | W / m*K | 导热系数 |
| ρ | 1 | kg / m 3 | 密度 |
| L | 70.26 | J / kg | 汽化潜热 |
| T l | -0.15 | °C | 流体温度 |
| T 0 | 0 | °C | 初始温度 |
| T BC | -45 | °C | 温度边界条件 |
| L 1 | 4 | m | 长度 |
| t final | 2 | s | 仿真时长 |
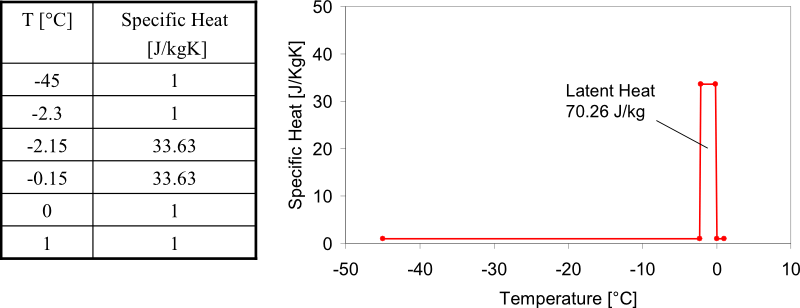
| T [°C] | 比热容 [J / kgK] |
|---|---|
| -45 | 1 |
| -2.3 | 1 |
| -2.15 | 33.63 |
| -0.15 | 33.63 |
| 0 | 1 |
| 1 | 1 |
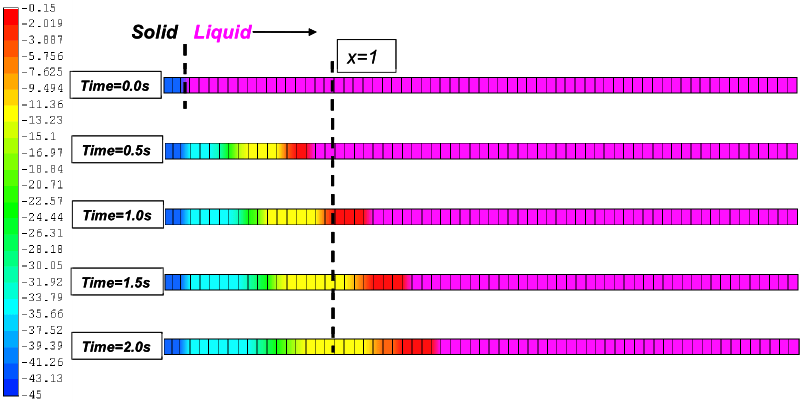
相变的标准测试问题是一维Stefan问题。该问题包括一个材料区域,长度为4米,最初保持在一个统一的温度,T0=0°C,这大于液相线温度Tl=-0.15°C。在时间零点,该区域的左侧,x=0,降低到低于固体温度的温度,到TBC=-45°C,导致凝固前沿扩散到材料上。所有其他表面都是绝热的。问题示意图如图8所示[2]。
THESEUS‑FE模型
在领域中使用64个PSHELL3元素解决了该示例。在左侧应用温度边界条件,材料比热性能由下表1所示。计算了相变温度区间为2度,凝固起始温度为-0.15度。
结果
将THESEUS‑FE结果与解析解进行了比较。我们发现大约有1度的差异,这是由于潜热附加的数值计算造成的。在自然界中,相变或潜热的增加是瞬间发生的。数值上,狄拉克脉冲函数不能进行模拟,因此我们通过一个2度的温度带应用了潜热加法。它将导致一个约1度方案错误的建模错误。
圆柱体辐射(开口灰体腔)
系统
系统和边界条件
| 参数 | 数值 | 单位 | 描述 |
|---|---|---|---|
| ε | 0.3 | 发射率 | |
| k 1 | 1.0 | W / m*K | 导热系数 |
| T 0 | 0 | K | 周围温度 |
| L | 4 | m | 长度 |
| D | 1 | m | 直径 |
| q | 200 | W / m 2 | 热流密度 |
问题描述
一个简单的加热外壳的圆管,两端开口,外表面绝热。对于管壁内表面和周围环境在0 K下的均匀热添加q=200 W/m2,我们计算了沿内表面的稳态温度分布,见参考书目[3]。
THESEUS‑FE模型
管的开口端是不反射的,假定它们是周围温度为0 K时的黑体。在THESEUS‑FE中,实现了三种主要的辐射热交换;对于目前的问题,所使用的模型是带灰体辐射的开口腔。灰体辐射考虑各网格的反射和吸收,并进行全角系数矩阵计算。在管壁内表面,应用的边界条件是背景温度和热通量。这是一个纯热辐射和传导问题;定义的材料特性是发射率ε和传导系数k。
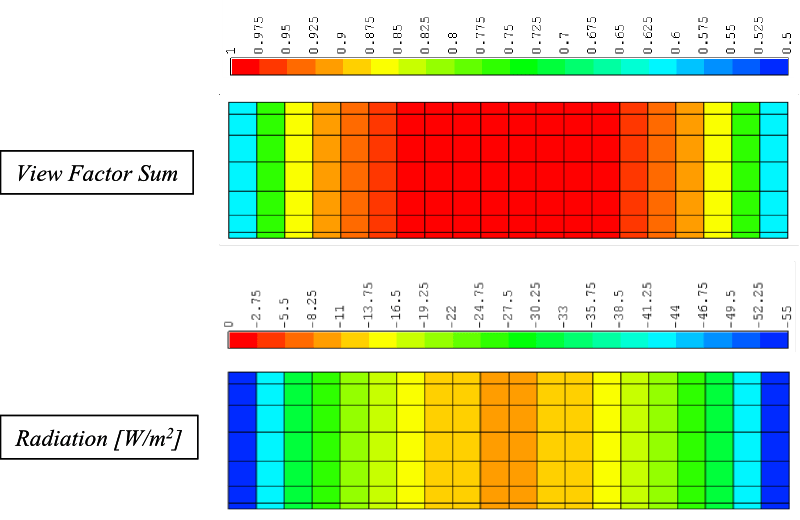
在下面的图像中,所显示的THESEUS‑FE结果是每个网格的角系数和、每个网格的辐射以及节点的温度值。
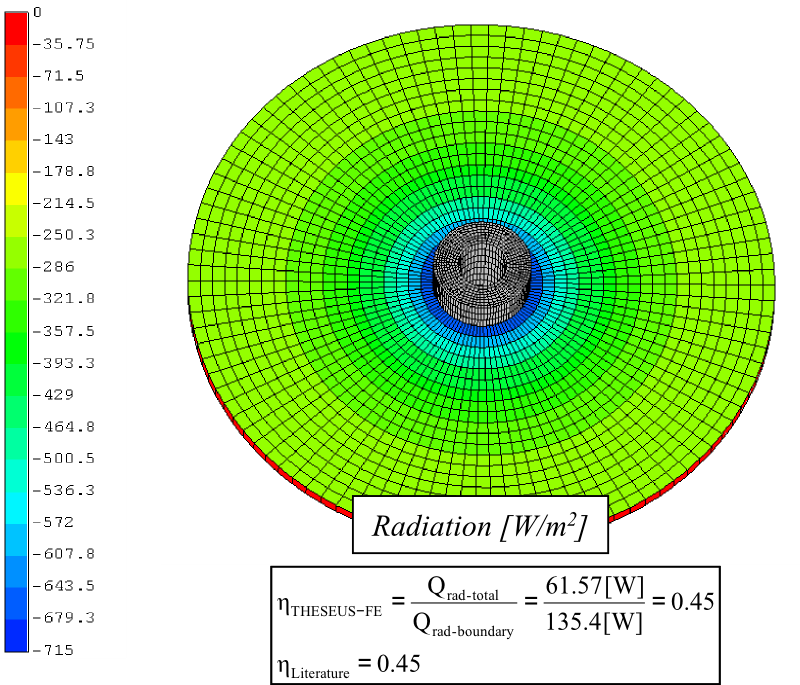
角系数是一个用来定义离开一个网格到达另一个网格的热功率的百分比。然后,每个网格上的角系数之和表示离开一个网格并到达域中所有其他网格的热功率的百分比。因此,对于封闭腔体,每个网格的角系数和等于1。对于开放的空腔,该值将小于1,这取决于损失了多少热能到环境中。辐射角系数很大程度上取决于距离,从结果可以看出,热功率主要在圆柱体端部损失,而从圆柱体中心损失的功率很少。最大和最小的角系数总和分别为0.975和0.6。
第二个图表量化了每个网格的辐射热损失量。对于靠近圆柱体端部的元件,其大小为-55 W/m2。
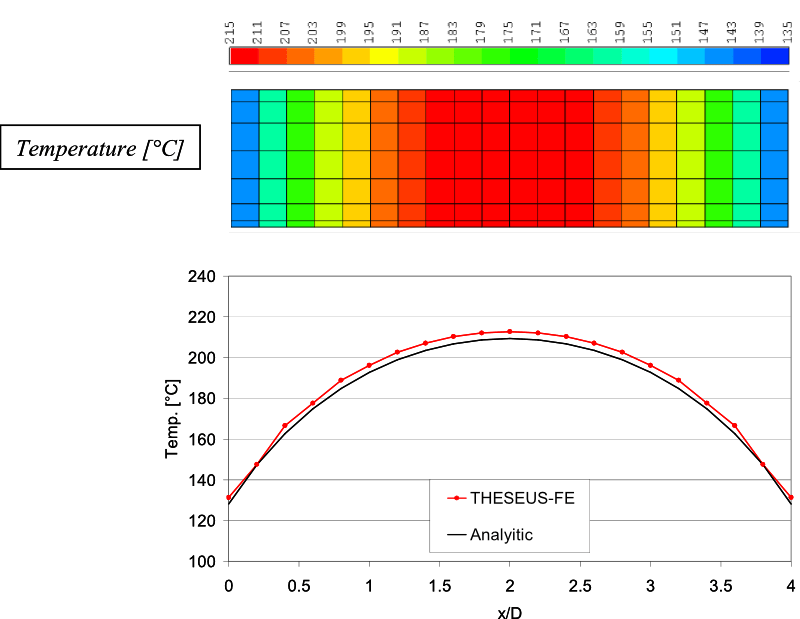
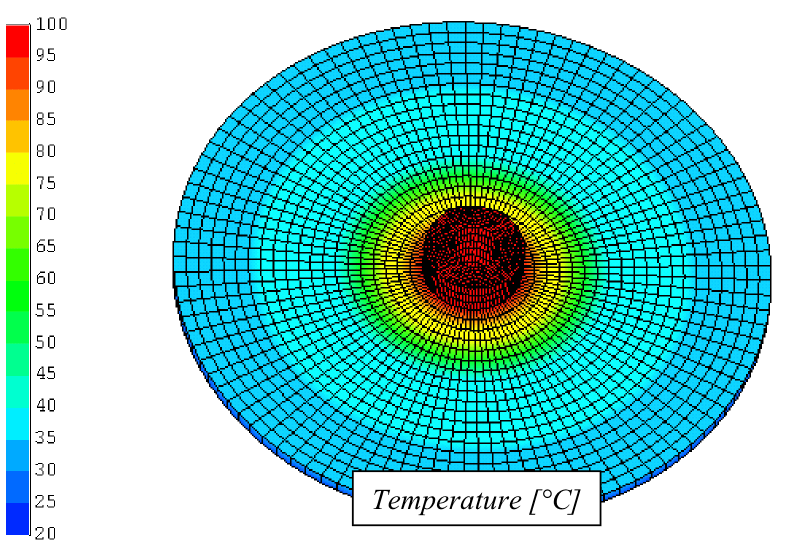
最后一张图显示了温度结果,并与解析解进行了比较。THESEUS‑FE分析结果与解析结果基本一致。我们可以进一步看到,热损失很少的圆柱中心与通过热辐射损失大部分热量的圆柱端部之间存在75度的温差。
结果
圆盘辐射
系统
系统和边界条件
| 参数 | 数值 | 单位 | 描述 |
|---|---|---|---|
| ε | 0.7 | 发射率 | |
| k | 15.0 | W / m*K | 导热系数 |
| T 0 | -273.15 | °C | 初始温度 |
| T BC | 100 | °C | 边界条件 |
| a | 0.01 | m | 厚度 |
| R i | 0.04 | m | 内部半径 |
| R 0 | 0.24 | m | 外部半径 |
问题描述
真空中的环形散热片的一面及其外缘周围绝热。该圆盘的厚度为0.01m,内半径为0.04m,外半径为0.24m,导热系数为15.0w/mk。能量由一根与中心孔相匹配的管道供应至内边缘,并将内边缘保持在100°C。暴露的环形表面为漫反射灰色,发射率为0.7,辐射至0 K处的环境,以研究在寒冷环境中的表现。结果表明,温度分布是沿圆盘径向位置的函数,每个网格的辐射通量和由THESEUS‑FE计算的圆盘辐射效率与文献[3]的结果进行了比较。
THESEUS‑FE模型
假设圆盘足够薄,因此考虑整个厚度的局部温度是恒定的。对于周边环境为零度时,没有入射辐射。在薄片内半径处规定温度边界条件,在薄片的底部和外边缘规定绝热条件,共4284个单元网格。此问题被看作一个瞬态问题计算,计算时间为6秒时达到稳态。
结果
一维圆柱辐射
系统
系统和边界条件
| 参数 | 数值 | 单位 | 描述 |
|---|---|---|---|
| k w | 24.0 | W / mK | 壁面导热系数 |
| ε | 1 | 壁面发射率 | |
| ρ f | 2 | kg / m 3 | 流体密度 |
| c p,f | 1 | kJ / kg*K | 流体比热容 |
| k f | 0.044 | W / m*K | 流体导热系数 |
| v f | 5E-5 | m / s | 流体入口速度 |
| h f | 3.4 | W / m 2 K | 流体对流换热系数 |
| T f,1 | 357 | °C | 流体入口温度 |
| q max | 1750 | W / m 2 | 最大应用热流密度 |
| l | 1 | m 2 K | 管长 |
| D o | 0.052 | m | 管外直径 |
| D i | 0.048 | m | 管内直径 |
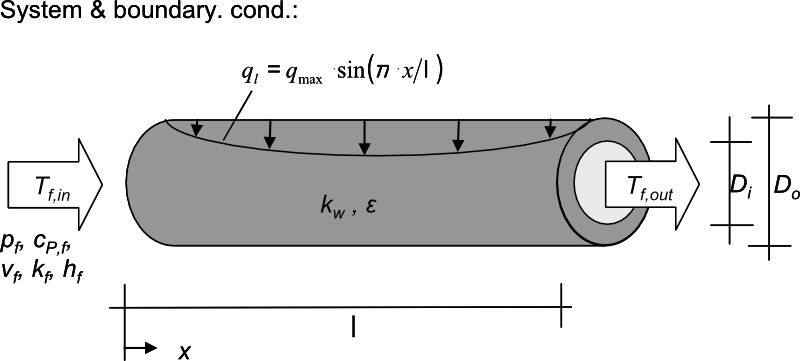
问题描述
入口温度为357°C的流体流过一个1米长的圆管,其内外直径分别为0.048米和0.052米。对流换热系数的计算基于管内的层流假设。流体的雷诺数为672,远低于2100-4000的过渡区。层流管的努塞尔数是常数,对流换热系数也是常数。
管外表面完全绝热,内表面以最大值1750 W/m2的正弦波热流进行电加热。管内壁被认为是一个黑体,并考虑了网格间的热辐射和网格与环境之间的热辐射。在这个问题中,我们考虑了对流、传导和热辐射的组合效应,并将壁面和沿轴向流动的温度结果与文献结果进行了比较。问题示意图如图17所示[3]。
THESEUS‑FE模型

THESEUS‑FE模型包含3115个厚度为0.002m的四边形PSHELL1网格。该域被划分为20个“体积”加上一个指定了入口流量条件的源体积。THESEUS‑FE中的“体积”是一个具有一个自由度的有界区域,Tvol,在整个体积中是恒定的。有限元和体积通过对流耦合。我们认为这面墙是一个黑色的物体(发射率=1),它吸收所有进入的能量。对于背景(环境)辐射温度,使用指定的入口流量温度和计算的出口流量温度。计算出流出温度后,更新辐射背景温度,重新进行计算。这一程序一直进行到流出温度达到收敛为止。在每个体积网格中,流体的对流、壁面内的传导以及壁面对环境和其他网格的热辐射的综合作用决定了壁面和流体的温度。在图18中,这些现象的相互作用被直观地显示出来。该问题被作为一个稳态问题进行计算。
结果
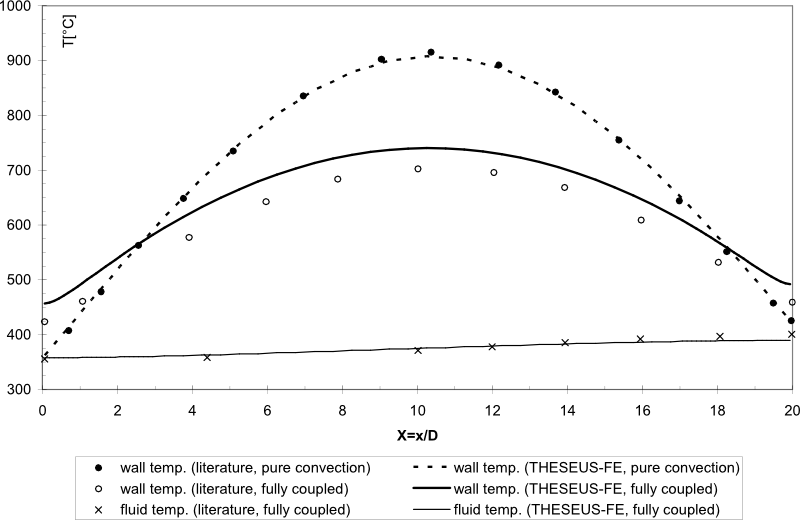
在图19中,我们比较了沿管长方向的THESEUS‑FE温度结果与文献中的结果。我们可以看到,完全耦合问题(辐射、传导和对流)的流体温度与文献的结果非常接近。对于壁面温度,对于完全耦合问题和纯对流问题的结果显示,忽略了辐射和传导。
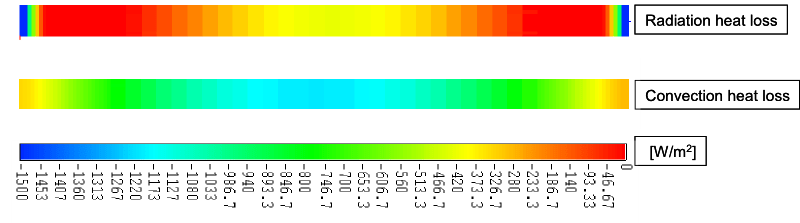
为了进一步分析这一问题,在图20中,我们比较了每个网格的辐射热损失和对流热损失。在管的进出口附近,热损失受到辐射的强烈驱动,而通过管的中心对流起主导作用。
参考书目
| [1] | HAUSE G., STIEGEL H. "Wärmebrücken Atlas für den Mauerwerksbau", Baueverlag. |
| [2] | REDDY, J.N., GARTLING, D.K. The Finite Element Method in Heat Transfer and Fluid Dynamics 2nd Edition. Boca Raton: CRC Press LLC, 2000. |
| [3] | SIEGEL R., HOWELL J.R. 2002, "Thermal Radiation Heat Transfer", 4th Edition, Taylor & Francis. |


